排列硬币的三种解法

排列硬币
总共有 n 枚硬币，将它们摆成一个阶梯形状，第 k 行就必须正好有 k 枚硬币。给定一个数字 n，找出可形成完整阶梯行的总行数。n 是一个非负整数，并且在32位有符号整型的范围内。
示例 1：

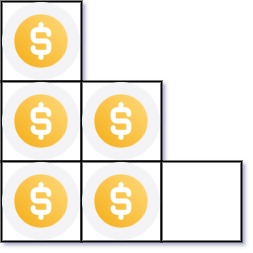
输入：n = 5
输出：2
解释：因为第三行不完整，所以返回 2 。
示例 2：

输入：n = 8
输出：3
解释：因为第四行不完整，所以返回 3 。
解法一：迭代
从第一行开始排列，排完一列、计算剩余硬币数，排第二列，直至剩余硬币数小于或等于行数
解法二：二分查找
假设能排 n 行，计算 n 行需要多少硬币数，如果大于 n，则排 n/2行，再计算硬币数和 n 的大小关系
解法三：牛顿迭代
使用牛顿迭代求平方根，(x + n/x)/2
假设能排 x 行 则 1 + 2 + 3 + …+ x = n，即 x(x+1)/2 = n 推导出 x = 2n – x

package od;

/**
 * 排列硬币（3种解法）
 * 总共有 n 枚硬币，将它们摆成一个阶梯形状，第 k 行就必须正好有 k 枚硬币。
 * 给定一个数字 n，找出可形成完整阶梯行的总行数。
 * n 是一个非负整数，并且在32位有符号整型的范围内。
 * 原文地址：https://www.codernav.com/2832.html
 * 更多算法详解：https://www.codernav.com
 */
public class OdTest27 {
    public static void main(String[] args) {
        // 解法一：迭代
        System.out.println(f1(10));
        // 解法二：二分.查找
        System.out.println(f2(10));
        // 解法三：牛顿.迭代
        System.out.println(f3(10));
    }

    public static int f1(int n) {
        // i代表第i行，也代表这行有i个硬币
        for (int i = 1; i <= n; i++) {
            // n代表剩余硬币数量
            n = n - i;
            // 剩余硬币个数小于这行需要的硬币个数
            if (n <= i) {
                return i;
            }
        }
        return 0;
    }

    public static int f2(int n) {
        int low = 0, high = n;
        while (low <= high) {
            long mid = (high - low) / 2 + low;
            long cost = ((mid + 1) * mid) / 2;

            if (cost == n) {
                return (int) mid;
            } else if (cost > n) {
                high = (int) mid - 1;
            } else {
                low = (int) mid + 1;
            }
        }
        return high;
    }

    public static int f3(int n) {
        if (n == 0) {
            return 0;
        }
        return (int) sqrts(n, n);
    }

    public static double sqrts(double x, int n) {
        double res = (x + (2 * n - x) / x) / 2;
        if (res == x) {
            return x;
        } else {
            return sqrts(res, n);
        }
    }

}